분류: 스택(monotonic stack) /
문제
문제 설명
히스토그램에 대해서 알고 있는가? 히스토그램은 아래와 같은 막대그래프를 말한다.
각 칸의 간격은 일정하고, 높이는 어떤 정수로 주어진다. 위 그림의 경우 높이가 각각 2 1 4 5 1 3 3이다.
이러한 히스토그램의 내부에 가장 넓이가 큰 직사각형을 그리려고 한다. 아래 그림의 빗금 친 부분이 그 예이다. 이 직사각형의 밑변은 항상 히스토그램의 아랫변에 평행하게 그려져야 한다.
주어진 히스토그램에 대해, 가장 큰 직사각형의 넓이를 구하는 프로그램을 작성하시오.
입력
첫 행에는 N (1 ≤ N ≤ 100,000) 이 주어진다. N은 히스토그램의 가로 칸의 수이다. 다음 N 행에 걸쳐 각 칸의 높이가 왼쪽에서부터 차례대로 주어진다. 각 칸의 높이는 1,000,000,000보다 작거나 같은 자연수 또는 0이다.
출력
첫째 줄에 가장 큰 직사각형의 넓이를 출력한다. 이 값은 20억을 넘지 않는다.
풀이
#include <iostream>
#include <stack>
using namespace std;
struct rect { int idx, h; };
int main(){
ios::sync_with_stdio(0); cin.tie(0);
int n; cin >> n;
int ans = 0;
stack<rect> S;
for(int i = 0; i <= n; i++){
int h = 0, idx = i;
if(i != n) cin >> h;
while(!S.empty() && S.top().h > h) {
idx = S.top().idx;
ans = max(ans, S.top().h * (i - idx));
S.pop();
}
if(S.empty() || S.top().h != h)
S.push({idx, h});
}
cout << ans;
}`Monotonic decreasing stack`
새로운 막대(`h`)가 입력되면 스택에 저장된 `h`보다 큰 막대로 만들어지는 직사각형들의 넓이이를 계산해 최댓값을 찾는 방법입니다.
각 막대의 높이를 오른쪽으로 연장해 가로길이를 계산한다고 생각해 봅시다. 자기보다 크거나 같은 높이의 막대가 나오면 가로가 계속 연장되고 자기보다 작은 막대가 나오면 연장되던 가로 길이가 끊기게 되어 시작 막대(가장 왼쪽에 있는 막대, 높이의 시작)의 높이로 만들 수 있는 직사각형의 크기가 확정됩니다. for 문을 돌며 스택의 변화와 답이 계산되는 과정을 살펴봅시다.

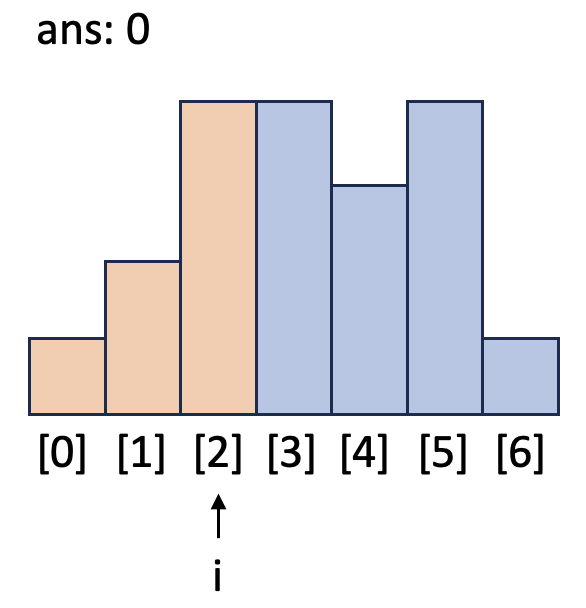
먼저 i=0에서 3까지 스택이 비어있거나 `h`가 `top`보다 크므로 while문이 실행되지 않고 막대들은 스택에 저장(`push`)됩니다. 이때까지는 높이가 작아지지 않아 넓이를 계산하지 않습니다. 현재까지 [0]의 가로길이는 3, [1]의 가로길이는 2, [2]의 가로길이는 1로 계속 연장 중입니다.

i = 3일 때 `h`가 `top`과 같으므로 아무런 일도 일어나지 않고 무시됩니다.
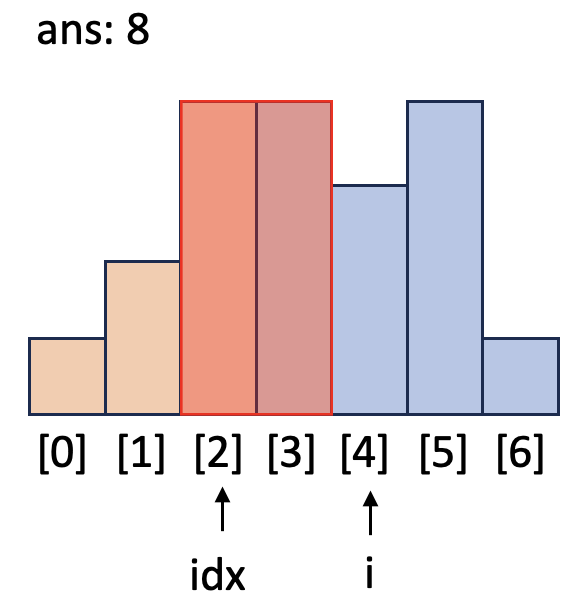

i = 4일 때 드디어 스택의 `top`보다 작은 `h`가 입력으로 주져 넓이가 계산됩니다.
[2]의 가로길이가 확정되고 [2]로 만들 수 있는 직사각형의 최대 넓이가 확정됩니다.
[2]의 높이와 가로길이로 넓이를 계산하고 [2]를 스택에서 제거(`pop`)합니다.
그다음 `top`인 [1]은 `h`보다 작으므로 while문이 끝나고 `idx`(마지막으로 `pop`한 자리)인 [2]와 `h`를 스택에 저장(`push`)합니다.

i = 5 역시 `top`이 `h`보다 크므로 while문을 실행하지 않고 스택에 저장하고 넘어갑니다.



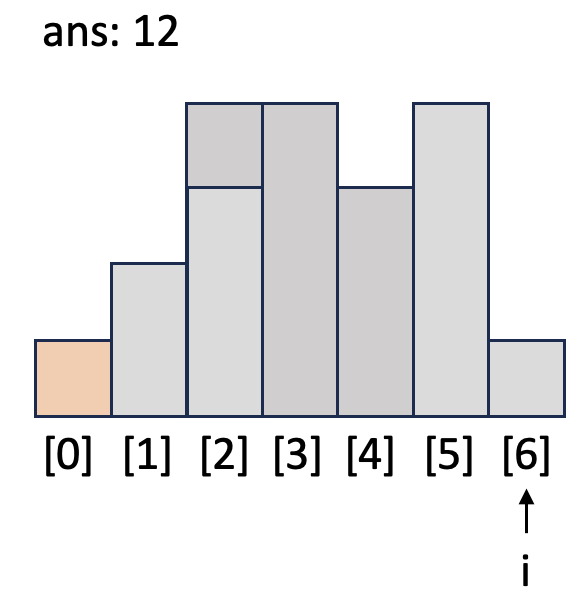
i = 6일 때 while 문을 돌며 `h`보다 작거나 같은 막대가 나올 때까지 넓이를 계산합니다. `idx`가 1이 되어서야 `h`와 같은 높이가 막대([0])를 발견하고 while문이 종료됩니다. `top`인 [0]과 `h`의 높이가 같으므로 `h`는 버립니다.

for문을 잘 보시면 i=0부터 i=n까지 총 n+1번 반복되고 i=n일 때 높이가 0인 막대를 집어넣어 남아있는 스택을 비우는 작업을 수행해 줍니다. 이것으로 각 막대로 만들 수 있는 가장 큰 직사각형을 모두 계산했습니다. 다시 올려보며 빨간 사각형을 보며 확인해 보세요.
'Problem Solving > BOJ' 카테고리의 다른 글
| [백준 - 6198] 옥상 정원 꾸미기 - C++ (0) | 2023.09.23 |
|---|---|
| [백준 - 17298] 오큰수 - C++ (1) | 2023.09.23 |
| [백준 - 2493] 탑 - C++ (0) | 2023.09.21 |
| [백준 - 1874] 스택 수열 - C++ (0) | 2023.09.20 |
| [백준 - 10828] 스택 - C++ (0) | 2023.09.19 |


