렌즈의 공식과 파이썬을 이용해 객체의 위치에 따른 상의 위치를 계산해보자.
Lens equation
렌즈의 공식은 렌즈의 초점거리, 렌즈의 중심으로부터 피사체의 거리, 렌즈의 중심으로부터 상 사이의 거리사이의 관계를 나타낸다. 이를 이용해 렌즈의 특성으로 알 때 렌즈와 와 객체 사이의 거리를 계산해 상이 맺히는 곳을 계산 할 수 있다.
Plotting graphs showing lens equation


import numpy as np
import matplotlib.pyplot as plt
## function
# s' = Lens_Equation(s,f)
# input
# f: focal length
# s: object location
# output
# s': image location
def Lens_Equation(s,f):
return (f*s)/(s+f)
def Lens_Equation_array(s,f):
if any(s < 0):
s1 = s[s<0]
s2 = s[s>=0]
img_loc1 = Lens_Equation(s1,f)
img_loc2 = Lens_Equation(s2,-f)
img_loc = np.concatenate([img_loc1,img_loc2])
else:
img_loc = Lens_Equation(s,f)
return img_loc
obj_loc = np.linspace(-1000,1000,1001) # cm
focal_length = 20 # cm
img_loc = Lens_Equation(obj_loc,focal_length)
valid_obj_loc = obj_loc[(obj_loc < 0) & (img_loc>0)]
real_img_loc = img_loc[(obj_loc < 0) & (img_loc>0)]
# plot: -10m ~ 10m
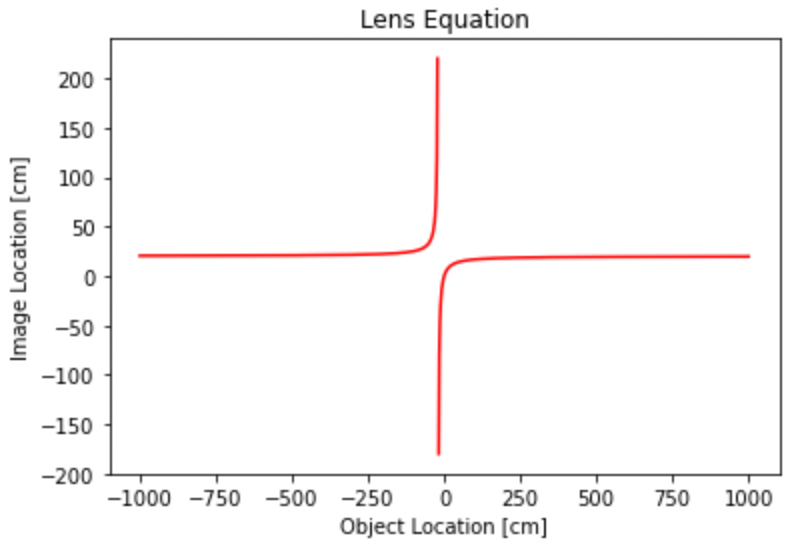
plt.plot(obj_loc, img_loc, 'r-')
plt.title('Lens Equation')
plt.xlabel('Object Location [cm]')
plt.ylabel('Image Location [cm]')
plt.show()
# plot: zoom
plt.axvline(x=-focal_length, color = 'c')
plt.axhline(y=focal_length, color = 'c')
plt.plot(obj_loc, img_loc, 'r-')
plt.title('Lens Equation Zoom')
plt.xlabel('Object Location [cm]')
plt.ylabel('Image Location [cm]')
plt.xlim(-140,100)
plt.ylim(-100,140)
plt.show()
#plot: valid value when the sensor location is positive
plt.axvline(x=-focal_length, color = 'c')
plt.axhline(y=focal_length, color = 'c')
plt.plot(valid_obj_loc, real_img_loc, 'r-')
plt.title('Valid Value (When sensor location is positive)')
plt.xlabel('Object Location [cm]')
plt.ylabel('Image Location [cm]')
plt.xlim(-150,50)
plt.ylim(-20,150)
plt.show()

# both sign focus
img_loc = Lens_Equation_array(obj_loc,focal_length)
valid_obj_loc = obj_loc[obj_loc*img_loc < 0]
real_img_loc = img_loc[obj_loc*img_loc < 0]
# plot -10m ~ 10m
plt.plot(obj_loc, img_loc, 'r-')
plt.title('Lens Equation Both Sign')
plt.xlabel('Object Location [cm]')
plt.ylabel('Image Location [cm]')
plt.show()
# plot zoom
plt.axvline(x=0, color = 'b')
plt.axhline(y=0, color = 'b')
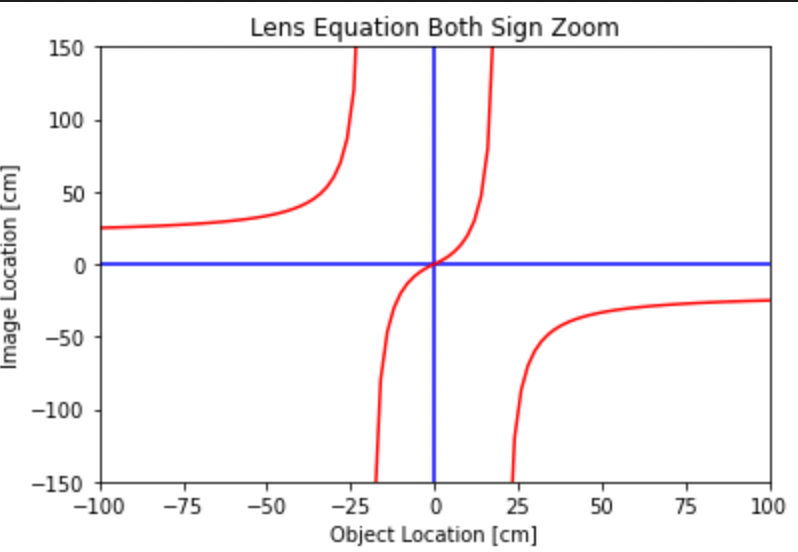
plt.plot(obj_loc, img_loc, 'r-')
plt.title('Lens Equation Both Sign Zoom')
plt.xlabel('Object Location [cm]')
plt.ylabel('Image Location [cm]')
plt.xlim(-100,100)
plt.ylim(-150,150)
plt.show()
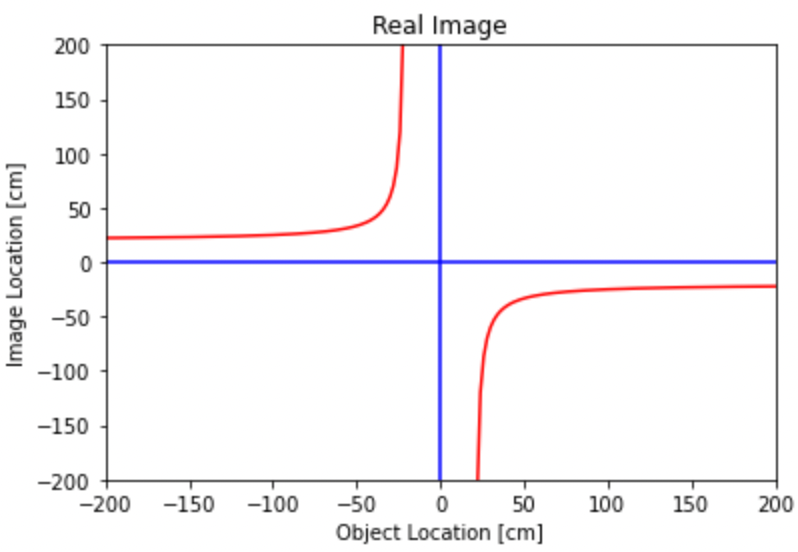
#plot the region in which a real image can acquired
plt.axvline(x=0, color = 'b')
plt.axhline(y=0, color = 'b')
plt.plot(valid_obj_loc, real_img_loc, 'r-')
plt.title('Real Image')
plt.xlabel('Object Location [cm]')
plt.ylabel('Image Location [cm]')
plt.xlim(-200,200)
plt.ylim(-200,200)
plt.show()
In an optical system
Program that computs the position of the image point in an optical system including a series of lens.


def Lens_Equation_both_sign(s,f):
if s<0:
img_loc = Lens_Equation(s,f)
else:
img_loc = Lens_Equation(s,-f)
return img_loc
# read file
params = []
with open('lens_info.txt', 'r') as file:
for line in file:
params.append(line.split('%')[0].strip())
# set parameters
obj_loc2 = int(params[0])
no_lens = int(params[1])
lens_loc = []
focal_len = []
for i in range(0,no_lens):
lens_loc.append(int(params[2+2*i]))
focal_len.append(int(params[2+2*i+1]))
lens_loc2 = np.array(lens_loc)
focal_len = np.array(focal_len)
# calculate example image locaion
img_loc2 = obj_loc2
for i in range(0,no_lens):
img_loc2 = img_loc2 - lens_loc[i]
img_loc2 = Lens_Equation_3(img_loc2,focal_len[i])
print(img_loc2)
# calculate image locaion
img_loc3 = obj_loc
img_loc3 = np.array(img_loc3)
for i in range(0,no_lens):
img_loc3 = img_loc3 - lens_loc[i]
img_loc3 = Lens_Equation_array(img_loc3,focal_len[i])
#plot
plt.plot(obj_loc, img_loc3, 'r-')
plt.title('Image')
plt.xlabel('Object Location [cm]')
plt.ylabel('Image Location [cm]')
#plt.xlim(-200,200)
plt.show()
#plot zoom
plt.plot(obj_loc, img_loc3, 'r-', label = 'spctrum')
plt.plot(obj_loc2, img_loc2, 'b*', label = 'example')
plt.title('Image Zoom')
plt.xlabel('Object Location [cm]')
plt.ylabel('Image Location [cm]')
plt.legend()
plt.xlim(-100,100)
plt.show()
'etc.' 카테고리의 다른 글
| Stefan-Boltzman law (using Python) (0) | 2021.11.08 |
|---|---|
| Wien's displacement law (using Python) (0) | 2021.11.08 |
| Planck's blackbody radiation law (using Python) (0) | 2021.11.08 |
